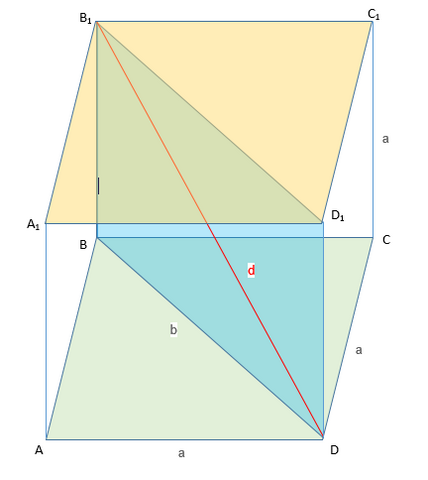
1. Найдите площадь диагонального сечения, площадь полной поверхности и объем куба, диагональ которого равна 1)3м 2) 6 дм
Треугольник BB₁D прямоугольный. По т.Пифагора
d²=a²+b²
Треугольник ABD прямоугольный. По т.Пифагора
b²=a²+a²
b=a√2
Треугольник BB₁D прямоугольный. По т.Пифагора
d²=a²+b²
d²=a²+(a√2)²=a²+2a²=3a²
a²=d²/3
a=d/√3
Диагональное сечение - прямоугольник со сторонами a, b. Его площадь
S₁=a*b=a*a√2=a²√2=a²=d²/3*√2=(d²√2)/3
Площадь полной поверхности равна 6 площадей грани. Грань - квадрат со стороной а
S₂=6a²=6d²/3=2d²
Объем куба
V=a³=(d/√3)³=d³/(3√3)
1) d=3м
S₁=(d²√2)/3=3√2 (м²)
S₂=2d²=2*9=18 (м²)
V=d³/(3√3)=9/√3=3√3 (м³)
2) d=6дм
S₁=(d²√2)/3=12√2 (дм²)
S₂=2d²=2*36=72 (дм²)
V=d³/(3√3)=6³/√3=36*6√3/3=72√3 (дм³)
2
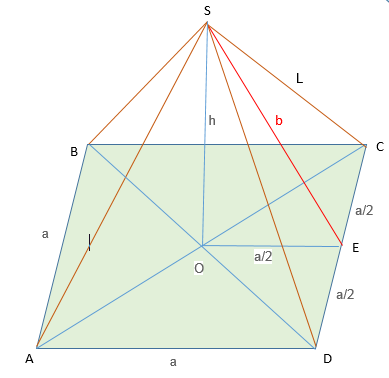
В правильной четырехугольной пирамиде сторона основания а
, высота h
, боковое ребро L. Найдите площади её боковой и полной поверхности и объем, если
1) а
= 2 см
h
= 4 см
2) а=6 дм
L
- 5 дм
Треугольник DSC равнобедренный Его высота b является и медианой, и биссектриссой.
1) Треугольник SOE прямоугольный. По т.Пифагора
b²=h²+(a/2)²
b²=4²+(2/2)²=16+1=17
b=√17
Площадь одной боковой грани - это площадь треугольнка 1/2*ab=1/2*2*√17=√17
Площадь боковой поверхности - это площадь 4-х таких треугольников
S₁=4√17 (см²)
Площадь полной поверхности это площадь боковой поверхности плюс площадь основания - квадрата со строрной а
S₂=S₁+a²=4√17+2²=4(1+√17) (см²)
Объем пирамиды
V=1/3*h*a²=1/3*4*2²=16/3 (см³)
2) Треугольник SEC прямоугольный. По т.Пифагора
b²=L²-(a/2)²
b²=5²-(6/2)²=25-9=16
b=4
Площадь одной боковой грани - это площадь треугольнка 1/2*ab=1/2*6*4=12
Площадь боковой поверхности - это площадь 4-х таких треугольников
S₁=4*12=48 (дм²)
Площадь полной поверхности это площадь боковой поверхности плюс площадь основания - квадрата со строрной а
S₂=S₁+a²=48+6²=84 (дм²)
Треугольник SOE прямоугольный. По т.Пифагора
h²=b²-(a/2)²
h²=16-9=7
h=√7
Объем пирамиды
V=1/3*h*a²=1/3*√7*6²=12√7/3 (дм³)