Вот решение С4 выложил, извини, что долго.
C6
Задача можно переформулировать так: при каких значениях параметра b уравнение
btg^2 x = 6 - cos x - b
имеет хотя бы одно решение.
Перенесу b влево и вынесу его за скобки:
btg^2 x + b = 6 - cos x
b(1+tg^2 x) = 6 - cos x
Вспоминаем о том, что 1 + tg^2 x = 1/cos^2 x, получаем
b/cos^2 x = 6 - cos x
Теперь напрашивается замена. Пусть cos x = t, |t| <= 1<br>Тогда получаем уравнение
b/t^2 = 6 - t
Перенесём всё влево и приведём всё к общему знаменателю:
b/t^2 - 6 + t = 0
(b-6t^2+t^3)/t^2 = 0
Дробь равна 0 тогда и только тогда, когда числитель равен 0, знаменатель не равен 0. Отсюда получаем, что
t^3 - 6t^2 + b = 0, t не равно 0.
Таким образом, задача сводится к следующей: найти все значения параметра b, при каждом из которых уравнение t^3 - 6t^2 + b = 0 имеет корни такие, что -1<= t <= 1, t не равен 0<br>1)Пусть t = 0, тогда b = 0 - не подходит.
2)Теперь пусть t не равно 0. Надо определить, при каких b уравнение имеет хотя бы один корень из отрезка [-1;1]. Я решал эту задачу графически.
t^3 - 6t^2 + b = 0
t^3 - 6t^2 = -b
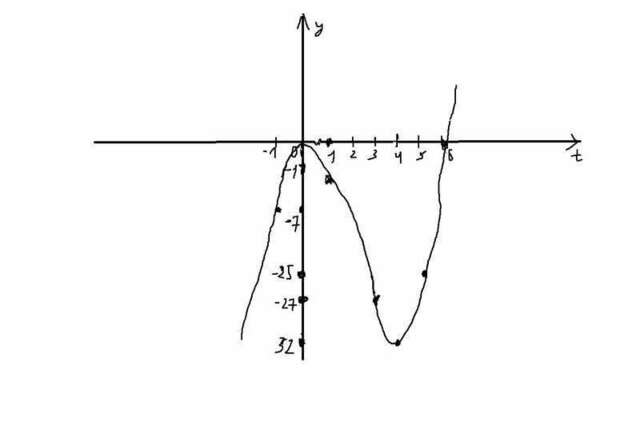
Построим график левой части. Для того чтобы построить его, предварительно проведём краткое исследование графика.(Эскиз я изобразил на рисунке)
Пусть h(t) = t^3 - 6t^2.
1)D(h) = R
2)h(t) = 0
t^3 - 6t^2 = 0
t^2(t-6) = 0
t = 0 или t = 6
Итак, точки пересечения с осью Ot: t = 0 и t = 6.
3)Найдём точки пересечения с осью OY:
t = 0, если y = 0.
4)Исследуем функцию h(t) на монотонность, найдём её точки максимума и минимума.
1)h'(t) = 3t^2 - 12t
2)h'(t) = 0 3t^2 - 12t = 0
3t(t - 4) = 0
t = 0 или t = 4
Функция возрастает на (-беск;0] и на [4;+беск)
Функция убывает на [0;4]
По построенному графику видно, что условие задачи выполняется, когда -7 <= -b < 0, откуда находим искомые значения b.<br>