Тут считать придется очень много. И желательно правильно. Сначала надо разобраться что к чему. Надо нарисовать первое н-во системы. Тут стоит модуль и знак меньше. По определению модуля:

Значит у нас будут 2 графика, но нам нужно будет сделать не совокупность, а систему, т.е. будет 1 промежуток. Где стоит -12 получается следующее:
 (1)
(1)
Где стоит 12:
 (2)
(2)
Чтобы нарисовать неравенство, надо нарисовать равенство. Сейчас попробую...
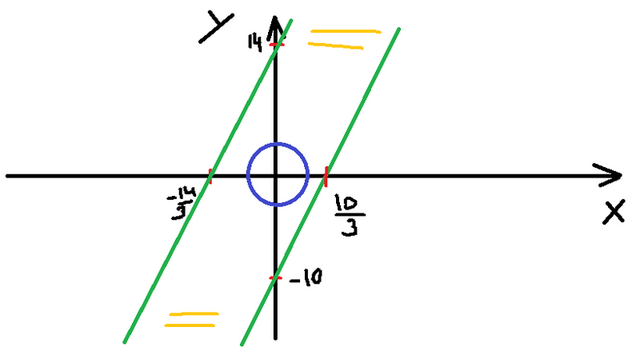
Как-то так. Ваши два графика. Интересует нас область которая между ними (я показал ее такими желтыми палочками). Также я нарисовал круг, который является 2 частью исходной системы. При а=0 он будет выглядеть именно так. Теперь ключевой момент. Точка вершины вашего "круга" будет ходить по прямой y=-x/3. Считается это так: при а=1 точки вершины: y=-1. x=3. тогда y=-x/3. Нам это важно, потому что нам надо знать, куда "поедет кружок". Чтобы было одно решение, кружок должен касаться одного из графиков неравенств. Просто потому, что при а=0 решений бесконечно много. Теперь придется это считать. Окружность касается прямой, когда дискриминант равен нулю. Рассмотрим касание левой прямой и окружности. Подставим значение y из (1) в уравнение окружности:

Формулу подсчета D/4 (если не знаете) можно легко найти в источниках.
Теперь второй случай. Делаем то же самое, но с (2):

Теперь у нас есть 4 значения а, но подходят не все. Если а=2, то вроде как все нормально, подходит. Если а=0,3, то мало что изменится (даже на моем горе-рисунке), не подходит. Из второй серии нам ничего не подходит, потому что:
Радиус больше(или равен) нуля. А у нас 3а+4 меньше нуля при а=-1,5. При а=-1 касание будет внутренним. Ответ:а=2.