В прямоугольный треугольник вписан квадрат, одна из вершин которого совпадает с вершиной...

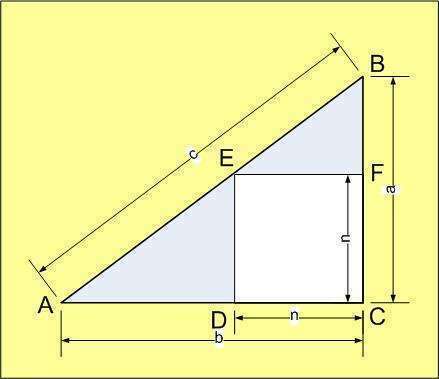
Рассмотрим ΔAEB и ΔEBF. Они подобны, поскольку все их углы равны (углы EFB и ACB прямые, а остальные попарно образованы параллельными прямыми, пересекающими третью).
Тогда можно записать пропорцию: AD/EF=ED/BF. (1)
Из чертежа AD=b-n; EF=n; ED=n; BF=a-n
Подставляя в (1) получим (b-n)/n=n/(a-n) (2)
Из условия задачи a=b-1
Периметр квадрата равен 4n, а по условию он равен 48/7, тогда n=12/7
Решим уравнение (2) относительно b - длины большего катета.
$\frac{b-n}{n}= \frac{n}{b-n-1}; \ (b-n)(b-n-1)=n^2; \\ b^2-bn-b-bn+n^2+n=n^2; \ b^2-2bn-b+n=0; \\ b^2-(2n+1)b+n=0; \\ D=(2n+1)^2-4n=4n^2+4n+1-4n= 4n^2+1; \\ n= \frac{12}{7} \to D=4*( \frac{12}{7})^2+1= \frac{4*144+49}{7^2}= \frac{25^2}{7^2}=( \frac{25}{7})^2; \\ b= \frac{1}{2}*(2n+1\mp \frac{25}{7})= \frac{1}{2}*(2* \frac{12}{7} +1\mp \frac{25}{7})=\frac{1}{2}*(\frac{31}{7}\mp \frac{25}{7})= \frac{31\mp 25}{14}; \\ b_1= \frac{3}{7}; \ b_2=4$
Значение b=3/7 не имеет геометрического смысла, поскольку получается, что bОстается ответ b=4.