Медианы в точке пересечения (обозначим её буквой К) делятся в отношении 2:1 считая от вершины.
Значит АК=2АМ/3, СК=2СN/3
Угол АКС треугольника АКС равен 180⁰-60⁰=120⁰.
Найдем площадь треугольника АКС:
S=(AK·KC·sin 120⁰)/2=(2AM/3·2СN/3·sin 120⁰)/2=(4/9 АМ·СN·√3/2)/2= =(8/9·√3/2)/2=2√3/9
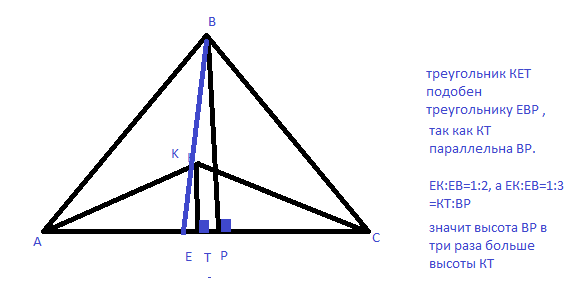
Площадь треугольника АВС в три раза больше, потому что основание этих треугольников одинаковое, а высота треугольника АВС в 3 раза больше высоты треугольника АКВ.(см. рисунок).
Ответ. 2√3/3