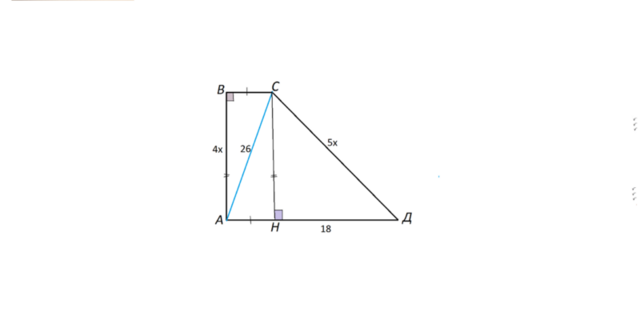
Обозначим вершины трапеции АВСД.
Из вершины С тупого угла трапеции опустим высотуСН на АД.
АВСН - прямоугольник ( т.к. трапеция прямоугольная).
ВС=АН,
АВ=СН.
Площадь трапеции равна произведению её высоты на полусумму оснований.
S АВСД=СН*(АД+ВС):2
Пусть коэффициент отношения боковых сторон равен х.
Тогда
АВ=4х,
СД=5х.
СН=АВ=4х.
Из прямоугольного треугольника СНД
НД²=СД²-СН²
18=√(25х²-16х²)=3х
х=НД:3=18:3=6 см
АВ=4х=4*6=24 см
АН=√(АС²-СН²)=10 см
ВС=АН=10 см
АД=10+18=28 см
S АВСД=СН*(АД+ВС):2
S АВСД=24*(28+10):2=456 см²