2sin^2(2x) < 1
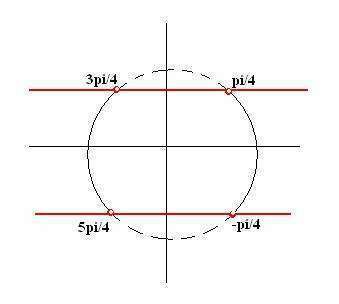
sin^2(2x) < 1/2<br>-√2/2 < sin(2x) < √2/2<br>Решим с помощью единичной окружности (см. рисунок).
Решением является:
3π/4 + 2πk < 2x < 5π/4 + 2πk, k∈Z
-π/4 + 2πk < 2x < π/4 + 2πk
3π/8 + πk < x < 5π/8 + πk, k∈Z
-π/8 +πk < x < π/8 + πk, k∈Z