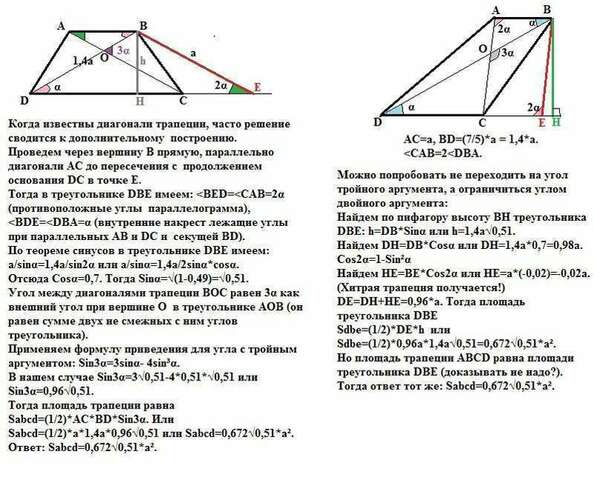
Когда известны диагонали трапеции, часто решение сводится к дополнительному построению.
Проведем через вершину В прямую, параллельно диагонали АС до пересечения с продолжением основания DC в точке Е.
Тогда в треугольнике DBE имеем: параллелограмма),
секущей ВD).
По теореме синусов в треугольнике DBE имеем:
а/sinα=1,4a/sin2α или а/sinα=1,4a/2sinα*cosα.
Отсюда Сosα=0,7. Тогда Sinα=√(1-0,49)=√0,51.
Угол между диагоналями трапеции ВОС равен 3α как внешний угол при вершине О в треугольнике АОВ (он равен сумме двух не смежных с ним углов треугольника).
Применяем формулу приведения для угла с тройным аргументом:
Sin3α=3sinα-4sin³α.
В нашем случае Sin3α=3√0,51-4*0,51*√0,51 или
Sin3α=0,96√0,51.
Тогда площадь трапеции равна
Sabcd=(1/2)*AC*BD*Sin3α. Или
Sabcd=(1/2)*а*1,4а*0,96√0,51 или Sabcd=0,672√0,51*a².
Ответ: Sabcd=0,672√0,51*a².
Можно попробовать не переходить на угол тройного аргумента, а ограничиться
углом двойного аргумента:
Найдем по Пифагору высоту ВН треугольника DBE: h=DB*Sinα или h=1,4a√0,51.
Найдем DH=DB*Cosα или DH=1,4a*0,7=0,98a.
Cos2α=1-Sin²α.
Найдем HE=BE*Cos2α или HE=a*(-0,02)=-0,02a. (Хитрая трапеция получается!)
DE=DH+HE=0,96*a. Тогда площадь треугольника DBE
Sdbe=(1/2)*DE*h или
Sdbe=(1/2)*0,96a*1,4a√0,51=0,672√0,51*a².
Но площадь трапеции АВСD равна площади треугольника DBE (доказывать не надо?).
Тогда ответ тот же: Sabcd=0,672√0,51*a².