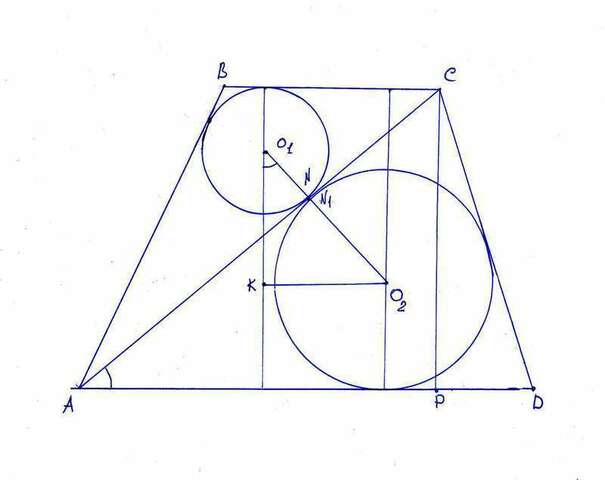
На чертеже точки касания N и N1 изображены совпадающими, но это еще надо доказать. Поэтому СНАЧАЛА я не считаю их совпадающими. То есть окружность O1 касается AC в точке N, а окружность O2 - в точке N1 (слова "с центром" дальше буду опускать, если и так ясно).
Для треугольника ABC точки касания с O1 делят стороны на три отрезка AN, CN и еще один (точнее, два равных) из вершины B. Я обозначу его например буквой x.
Тогда очевидно
AN + CN = AC;
AN + x = AB;
CN + x = BC;
Если вычесть из второго третье, получится AN - CN = AB - BC; если теперь сложить это с первым, то
AN = (AC + AB - BC)/2;
Точно так же для треугольника ACD получается
AN1 = (AC + AD - CD)/2; и нигде не предполагается, что AN = AN1; это надо доказать.
Весь четырехугольник ABCD является ОПИСАННЫМ, то есть AD + BC = AB + CD;
или AD - CD = AB - BC; или AC + AD - CD = AC + AB - BC; то есть AN = AN1, и точки N и N1 совпадают, это просто одна точка N.
Последствия этого очень велики. :) Окружности O1 и O2 касаются, AC является общей касательной, проведенной в точке касания N окружностей O1 и O2, и линия центров O1O2 перпендикулярна AC.
Важно! - пока нигде не использовано, что ABCD - трапеция! Этот результат справедлив для любого выпуклого описанного четырехугольника.
Поэтому (см. чертеж) ∠KO1O2 = ∠CAD (стороны углов перпендикулярны), и треугольники KO1O2 и ACP подобны. CP - высота трапеции. Она равна
CP = 2R = 40;
сумма радиусов окружностей равна O1O2 = 25; отсюда легко найти KO1 = 40 - 25 = 15; получился "египетский" треугольник :) то есть KO2 = 20;
Ну, и из подобия KO1O2 и ACP AC = 50 (поскольку СP = 2*KO2 :) )