Боковое ребро наклонной призмы равно 12 см и образует с плоскостью основания угол 60...

Question

Боковое ребро наклонной призмы равно 12 см и образует с плоскостью основания угол 60 градусов. Найти высоту призмы.

----

Диагональ равнобокой трапеции с основаниями 12 см и 20 см перпендикулярна к боковой стороне. Найти тангенс острого угла трапеции.

Answer 1

1)
h=d*sin(pi/3)=12*корень(3)/2 см =6*корень(3) см
2)
равнобокая(а значит имеет ось симметрии) трапеция ABCD
AД = 20
BC = 12
ДB - диагональ перпендикулярна AB
АС - диагональ перпендикулярна BД
значит около трапеции можно описать окружность, причем AД - диаметр
О - середина AД
искомый угол СДА
сответствующий ему центральный угол AOC
tg(СДА)=tg(AOC/2)=tg((pi/2+arcsin(6/10))/2)=
[ по формуле тангенс половинного угла ]
=sin(pi/2+arcsin(6/10))/(1+cos(pi/2+arcsin(6/10)))=
[ по формулам приведения ]
=cos(arcsin(6/10))/(1-sin(arcsin(6/10)))=(4/5) / (1-3/5)=2 - это ответ

Answer 2

1) Проведи высоту из верхней вершины призмы на основание.
Получится прямоугольный треугольник, у которого гипотенуза - это боковое ребро, равное 12 см, и угол 60 градусов. Высота - это катет напротив этого угла
H = b*sin 60 = 12*корень(3)/2 = 6*корень(3)

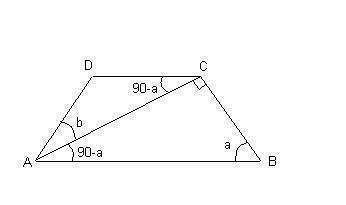
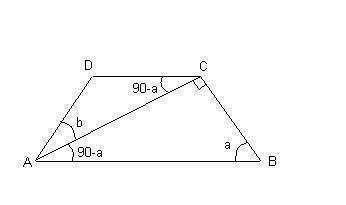
2) Смотри рисунок.
AB = 20, CD = 12, ACB = 90, ABC = DAB = a, BC = AD = AB*cos a, AC = d = AB*sin a
tg a = AC/BC
По теореме косинусов
AD^2 = AC^2 + CD^2 - 2*AC*CD*cos(90-a)
(AB*cos a)^2 = (AB*sin a)^2 + CD^2 - 2*AB*sin a*CD*sin a
400*cos^2 a = 400*sin^2 a + 144 - 2*20*12*sin^2 a = 144 - 80*sin^2 a
80sin^2 a + 400cos^2 a = 144
5sin^2 a + 25cos^2 a = 9
5sin^2 a + 5cos^2 a + 20cos^2 a = 9
20cos^2 a = 4
cos^2 a = 1/5
sin^2 a = 1 - cos^2 a = 1 - 1/5 = 4/5
tg^2 a = sin^2 a / cos^2 a = (4/5) : (1/5) = 4
tg a = 2

---

---