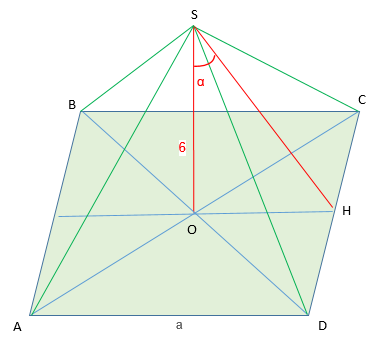
Треугольник SOH прямоугольный, Из определения тангенса
OH=SO·tgα=6tg30⁰=6/√3
ОН равна половине стороны квадрата основания
а=2*6/√3=12/√3
Апофема является гипотенузой. А в прямоугольном треугольнике она вдвое болше катета, лежащего напротив угла в 30⁰
SH=2OH=12/√3
Находим площадь боковой грани как площадь треугольника
S₁=1/2*a*h=1/2*12/√3*12/√3=1/2*144/3=72/3=24
Таких граней 4. Итого, площадь боковой поверхности
S=4S₁=4*24=96