Помогите пожалуйста!Определить результирующую силу, действующую ** выделенный заряд.

Question

Дан 1 ответ

TuW_zn · Answer 1 · 2018-03-18T21:34:16+0000

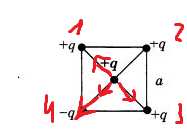
В 1ой задаче стоит заметить, что заряды 1 и 3 одинаково заряжены и у них одинаковое расстояние до пробного заряда . Это значит, что кулоновские силы отталкивания будут одинаковы у них (однако, направлены они будут в разные стороны) => их равнодействующая будет равна нулю (векторы просто наложатся друг на друга и нивелируются .
Значит, на наш пробник будут действовать только 2 оставшиеся силы. Со стороны заряда 2(положительного,он будет отталкивать его) и 4ого (он будет притягивать его ). Остаётся найти расстояние между пробником и этими двумя .(расстояние между пробником и зарядом 4 будет таким же,как и у пробника и 2ым)
Пробный заряд находится в центре квадрата на его диагонали и делит её пополам .Диагональ квадрата $a \sqrt{2}$ , где a = сторона квадрата. Значит, искомое расстояние - $\frac{ a\sqrt{2} }{2}$
Ну а дальше всё по той же схеме, что и в прошлой задаче, через закон кулона .
Выходит следующее $R = k\frac{q^2}{ {(\frac{{a\sqrt{2}}}{2})}^{2} } + k\frac{q^2}{ {(\frac{{a\sqrt{2}}}{2})}^{2} } = 2k\frac{q^2}{ {(\frac{{a\sqrt{2}}}{2})}^{2} } = 2k \frac{4{q}^{2}}{2{a}^{2}}= k \frac{8{q}^{2}}{2{a}^{2}}$

-------------------------------------------------------------------------------
2 задача.
всё по той же схеме ищем 2 силы,действующие на пробный заряд.
F1 со стороны положительного = $F2=k \frac{{4q}^{2}}{{a}^{2}}$
Со стороны отрицательного - $F2=k \frac{{q}^{2}}{{a}^{2}}$
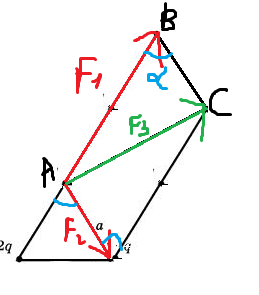
Равнодействующая будет находится из результирующего вектора , его ищем по правилу параллелограмма.
Искомый вектор силы будет диагональю, её ищем по теореме косинусов (рассматриваем треугольник ABC) , BC = F2.
Угол B= 60 градусов(и задаче дан равносторонний треугольник) .
$F3= \sqrt{{F1}^{2}+{F2}^{2}-2F1F2cos(60)}= \sqrt{{k}^{2} \frac{16{q}^{4}}{{a}^{4}} +{k}^{2} \frac{{q}^{4}}{{a}^{4}} - {k}^{2} \frac{4{q}^{4}}{{a}^{4}}} =$ $k\frac{{q}^{2}}{{a}^{2}} \sqrt{13}$