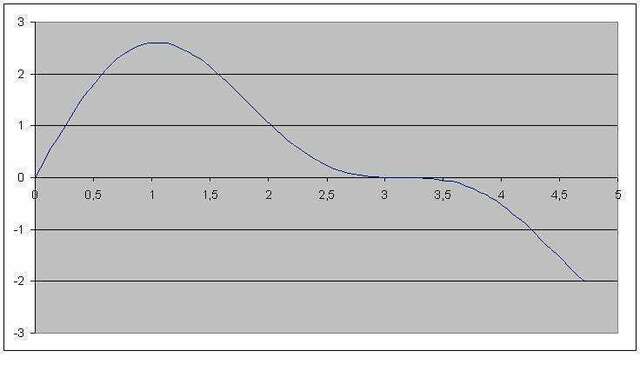
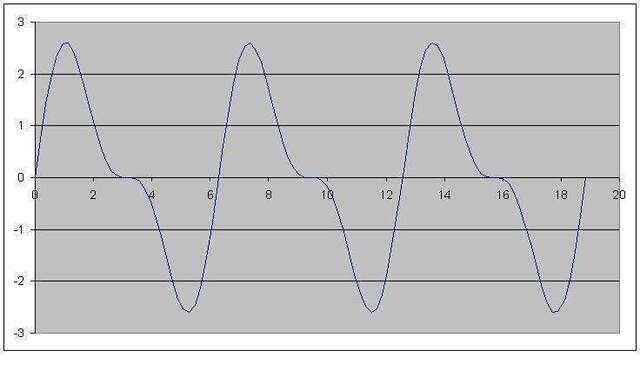
у = 2sinx + sin2x
y`=2cosx + 2cos2x=2*2*cos(3x/2)*cos(x/2)
y`=0 при 3x/2=pi/2+pi*k или x/2=pi/2+pi*n
x=pi/3+2pi*k/3 или x=pi+2pi*n
x=pi/3+2pi*k/3
минимальное и максимальное значение надо искать среди точек
x=0;x=pi/3;x=pi;x=3pi/2
y(x=0)= 2*sin(0) + sin(2*0)=0
y(x=pi/3)= 2*sin(pi/3) + sin(2*pi/3)=3*корень(3)/2 =
2,598076
- локальный максимум
y(x=pi)= 2*sin(pi) + sin(2*pi)=0
y(x=3*pi/2)= 2*sin(3*pi/2) + sin(2*3*pi/2)=-2 - локальный минимум
во вложении график на исследуемом участке и тот же график на более широком участке