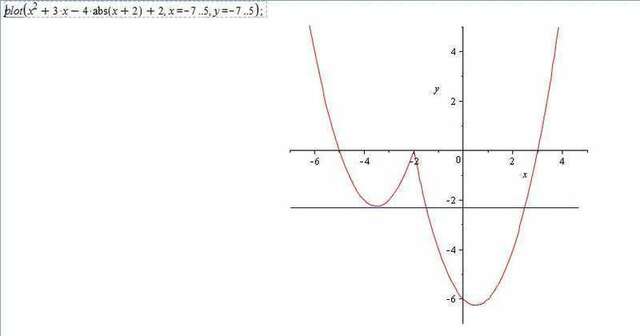
Во вложении - график функции.
Синим цветом показана одна из линий при m=2.25. Вторая линия совпадает с осью абсцисс (m=0).
Исходная функция  содержит функцию абсолютной величины, поэтому её надо рассматривать отдельно на участках, где выражение под знаком абсолютной величины отрицательно и положительно, т.е. на интервалах (-∞;-2] и [-2;+∞]
содержит функцию абсолютной величины, поэтому её надо рассматривать отдельно на участках, где выражение под знаком абсолютной величины отрицательно и положительно, т.е. на интервалах (-∞;-2] и [-2;+∞]
На первом интервале |x+2|≤0 и функция примет следующий вид:
y=x²+3x+4(x+2)+2 ⇒ y=x²+7x+10. График функции - квадратная парабола с ветвями, направленными вверх (коэффициент при х² положительный). Чтобы определить точки пересечения с осью абсцисс составим уравнение
x²+7x+10=0 ⇒ x1=-5; x2=-2 - это и будут точки пересечения графика функции с осью абсцисс.
На втором интервале |x+2|≥0 и функция примет следующий вид:
y=x²+3x-4(x+2)+2
⇒ y=x²-x-6. График функции - квадратная парабола с ветвями,
направленными вверх (коэффициент при х² положительный). Чтобы определить точки пересечения с осью абсцисс составим уравнение
x²-x-6=0 ⇒ x3=-2; x4=3 - это и будут точки пересечения графика функции с осью абсцисс.
Корни х2 и х3 совпали, это значит, что всего имеется три точки пересечения графиков с осью обсцисс в точках х1=-5б х2=-2б х3=3. Это и будет первая из искомых прямых, т.е. m1=0.
Построив и рассмотрев график функции, можно определить, что вторая прямая, параллельная оси абсцисс и имеющая с графиком функции ровно три общие точки - это прямая, проходящая через минимум первой из рассмотренных функций (показана на графике синим цветом). Для нахождения точки экстремума функции y=x²+7x+10 достаточно её производную приравнять нулю. y'=2x+7; 2x+7=0 ⇒ x=-3.5
Подставляя найденное значение x в выражение функции получим y=(-3.5)²-7*3.5+10=
-2.25, т.е. m2=-2.25.