везде на рисунках нужно поставить знак ↑
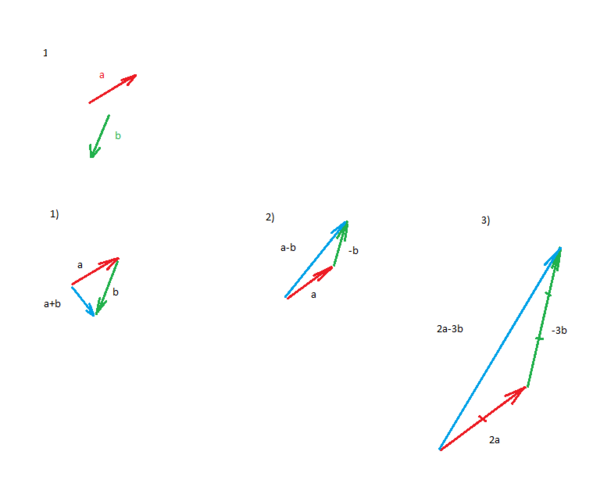
1.
1)↑a+↑b
2)↑a- ↑b
3)2↑a-3↑b
2.
найдите вектор СМ, если СА=а, СВ=b
CM=CA+AM=CA+1/3 AB=CA+1/3(AC++CB)=CA+1/3(-CA+CB)=CA-1/3CA-1/3CB=
=2/3CA-1/3CB=2/3*a -1/3b
3.
чтобы найти кооординаты вектора ↑d ↑d=↑a+↑b-↑c
надо сложить одноименные координаты векторов a,b,c
d(2+3+4; 3+0-3; -5+1+2)=d(9;0;-2)
длина вектора по теореме Пифагора для трехмерного измерения
берем координаты вектора d и считаем
|↑d|=√(9^2+0^2+(-2)^2)=√85
4.
A(3;2;-3)
B(5;1;-1)
C(1;-2;1)
по координатам вершин найдем длину сторон треугольника
длина проекции х(АВ)=|х(В)-х(А)|=|5-3|=2
длина проекции у(АВ)=|у(В)-у(А)|=|1-2|=|-1|=1
Длина проекции z(AB)=|z(B)-z(A)|=|-1-(-3)|=|-1+3|=2
длина отрезка |AB|=√(x^2+y^2+z^2)=√(2^2+1^2+2^2)=√9=3
и так далее
AB=3
BC=√((1-5)^2+(-2-1)^2+(1-(-1))^2)=√29
CA=√((3-1)^2+(2-(-2))^2+(-3-1)^2)=√36=6
Внутренний угол при вершине А находим по теореме косинусов
BC^2=AB^2+CA^2-2*AB*CA*cosA
cosA= (BC^2-AB^2-CA^2) / (-2*AB*CA)=( (√29)^2-3^2-6^2) /(-2*3*6) =-16 / -36=4/9
(sinA)^2=1-(cosA)^2
sinA= √(1-(4/9)^2= √(1-16/81)= √65/81= √65/9
площадь треугольника S=1/2*AB*CA*sinA=1/2*3*6*√65/9=√65