Формула радиуса шара, вписанного в конус:
R=Hr:(l+r)
R - радиус вписанного шара,
r - радиус основания конуса,
l - длина образующей конуса,
H - высота конуса
R=6·8:(10+8)=48:18
Подробное решение задачи ниже.
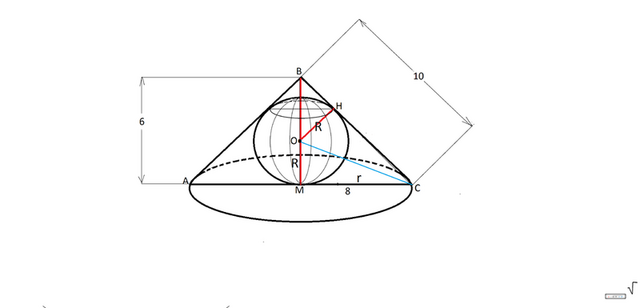
Шар, вписанный в конус, касается основания конуса в его центре, а боковой поверхности — по окружности.
Центр шара лежит на оси конуса.
Сделаем рисунок.
Сечение АВС шара плоскостью, проходящей через ось конуса и центр шара- равнобедренный треугольник.
ВМ- высота конуса.
ВС - образующая,
МС - радиус конуса,
ОМ=ОН - радиус вписанного шара.
Круг с центром О - вертикальное сечение шара.
МС по т. Пифагора =8
Центр вписанной в треугольник окружности находится на биссектрисе угла.
Центр О находится на СО - биссектрисе угла ВСМ.
Биссектриса треугольника делит противоположную сторону в отношении длин прилежащих сторон.
По свойству биссектрисы
ВО:ОМ=ВС:МС
ВО=6-R
(6-R):R=10:8 произведение крайних членов пропорции равно произведению ее средних членов:
48-8R=10R
18R=48
R=48:18=8:3=2 ²/₃
[email protected]