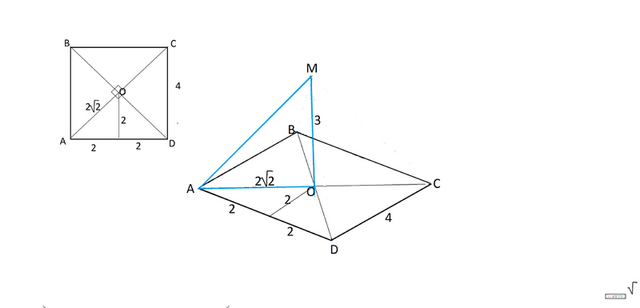
Так как О - точка пересечения диагоналей квадрата, а они при пересечении делятся пополам под прямым углом, - треугольник АОD прямоугольный равнобедренный, и АО равна половине диагонали квадрата.
Диагональ d=4√2
АО=2√2.
Половины диагоналей квадрата - проекции наклонных из М к каждой его вершине. Наклонные равны между собой, так как равны их проекции на плоскость квадрата. ⇒ Расстояние от каждой вершины квадрата до точки М одинаково.
АМ=ВМ=СМ=DМ
Из прямоугольного треугольника АМО по т. Пифагора
АМ=√(АО²+МО²)= √(8+9=√17 см
--------
b[email protected]