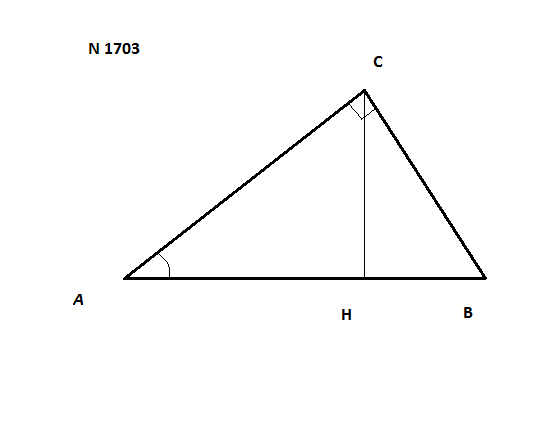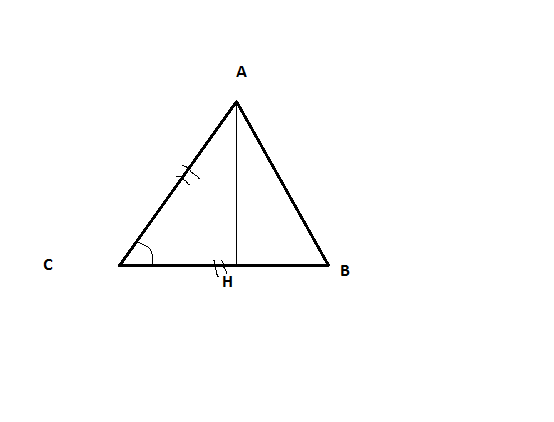1703
1. Найдем угол В, зная, что сумма углов треугольника равна 180°:
В = 180 - 30 - 90 = 60°
2. sinB = AC / AB, AC = sinB*AB
AC = sin60*AB = 32*√3/2 = 16√3
3. Рассмотрим прямоугольный треугольник АСН. Катет прямоугольного треугольника, лежащий против угла 30°, равен половине гипотенузы, значит:
СН = АС/2 = 8√3
4. По теореме Пифагора находим неизвестный катет АН в прямоугольном треугольнике АСН:
AH = √(6√3)² - (8√3)² = √576 = 24
5. Находим НВ:
НВ = АВ - АН = 32 - 24 = 8
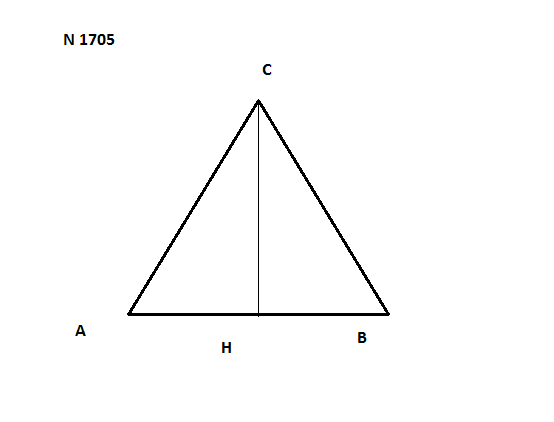
1705
1. В равностороннем треугольнике высота является и биссектрисой, и медианой. Значит, АН = НВ = АВ/2 = 54√3 / 2 = 27√3
2. По теореме Пифагора можно найти неизвестный катет СН в прямоугольном треугольнике АСН:
СН = √ AC² - AH² =√(54√3)² - (27√3)² = √2916*3 - 729*3 = √6561 = 81
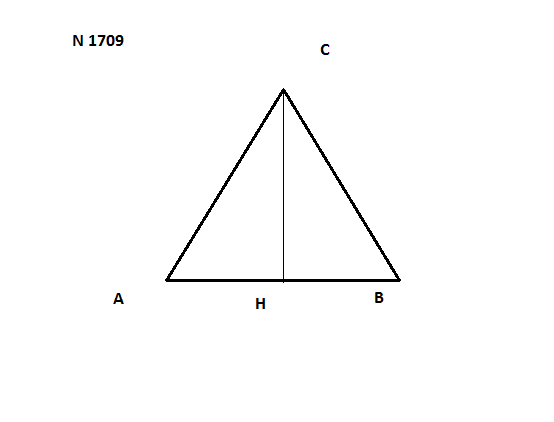
1709
1. В равностороннем треугольнике все углы равны 60. Зная это, запишем:
sinA = CH / AC, AC = CH / sin60,
AC = 39√3 : √3/2 = 39*2 = 78
Все стороны равностороннего треугольника равны по 78.
1710
1. В получившемся после построения высоты прямоугольном треугольнике САН катет АН, лежащий против угла в 30°, равен половине гипотенузы:
АН = АС / 2 = 22 / 2 = 11