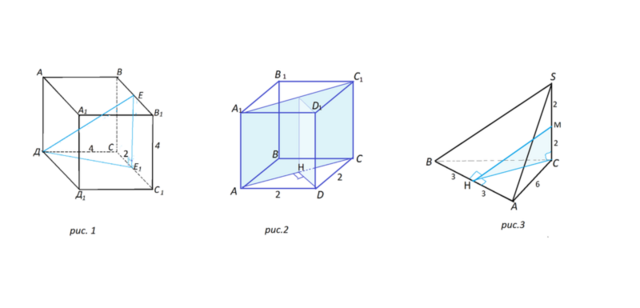
1) Длина ребра куба ABCDA₁B₁C₁D₁ равна 4 см. Точка Е - середина ребра ВВ₁. Вычислите длину ортогональной проекции отрезка ЕD на плоскость DD₁C₁.
См. рисунок 1
DЕ - наклонная к плоскости DD₁C₁.
Опустив перпендикуляр ЕЕ₁ на эту плоскость и соединив Е₁ с D, получим прямоугольный треугольник DЕЕ₁, в котором катет DЕ₁ является искомой проекцией. Он же является и гипотенузой прямоугольного треугольника DСЕ₁, катеты которого нам известны.
СЕ₁=ВЕ=4:2=2
DС=4
DЕ₁=√(16+4)=2√5 см
-----------------------------
2) Длина ребра куба АВСDA₁B₁C₁D₁ равна 2 см. Вычислите расстояние между прямой DD₁ и плоскостью АСС₁.
См. рисунок 2
Расстоянием от прямой до плоскости является перпендикуляр к плоскости из любой точки этой прямой.
DН - искомое расстояие.
DН- половина диагонали основания.
Диагональ основания равна 2√2, следовательно,
DН=√2 см
---------------------------
3) Основание треугольной пирамиды SABC является равносторонний треугольник, длина стороны которго равна 6 см. Боковое ребро SC перпендикулярно плоскости основания. Вычислите расстояние от середины ребра SC до прямой АВ, если известно, что SC = 4 см.
См. рисунок 3
Искомое расстояние - отрезок МН, перпендикулярный АВ.
По теореме о трех перпендикулярах его проекция также перпендикулярна АВ, и проекция эта является высотой СН правильного треугольника АВС.
СН=АС sin(60°)=3√3
МН по т. Пифагора равна корню из суммы квадратов катетов прямоугольного треугольника МСН ( МС, как часть SC, перпендикулярна плоскости АВС по условию).
МН=√(4+27)=√31 см
Ответ:расстояние от середины ребра SC до прямой АВ равно√31см