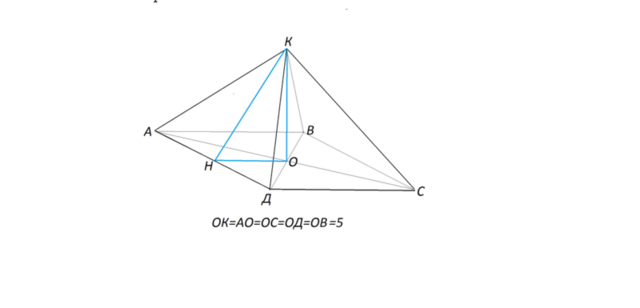
Найдите площадь правильной четырехугольной пирамиды, если центр ее основания удален от всех вершин на расстояние 5 единиц
См. рисунок.
Основание правильной четырехугольной пирамиды - квадрат.
Основание О
её высоты КО находится в центре пересечения диагоналей квадрата АВСД.
Так как центр основания удален от всех вершин пирамиды на равное расстояние,
высота пирамиды равна
АО - половине диагонали основания, т.е. радиусу описанной вокруг основания окружности, и
равна 5.
Сторону основания АВ=АД=ДС=ВС найдем из прямоугольного треугольника АОД
АД=АО√2
АД=
5√2
S АВСД=(5√2)²=
50 ед²
Площадь боковой поверхности равна половине произведения апофемы КН на периметр основания
КН=√(КО²+ОН²)
ОН=АД:2= (5√2):2
КН=√(5²+( 5√2):2)²)=√(25+50/4)=√(150):4)=
(5√6):2
S бок=4*КН*АД:2=2КН*АД=(5√6)*(5√2)=25√12=
50√3
Sполн= Sбок+Sосн=50√3+50=50(√3+1)