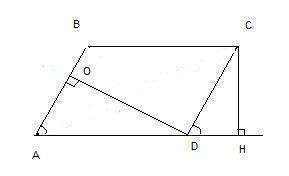
1. Построим перпендикуляр СН, чтобы показать расстояние между параллельными большими сторонами ВС и AD, и перпендикуляр DO, чтобы показать расстояние между меньшими сторонами АВ и CD. Найдем AD, зная площадь параллелограмма и его высоту СН:
Sabcd= AD*CH, отсюда
AD=S/CH=96/8=12 дм
2. Зная периметр, найдем АВ:
Pabcd=2AD+2AB, отсюда
AB=(P-2AD)/2=(44-24)/2= 10 дм
3. В прямоугольном треугольнике CHD найдем по теореме Пифагора DH:
DH = √DC²- CH²= √10² - 8² =√36 = 6 дм
4. Треугольники AOD и DНС подобны по первому признаку подобия: два угла одного треугольника соответственно равны двум углам другого. В нашем случае:5. Для подобных треугольников можно записать:
AD/CD=OD/DH, отсюда
OD=AD*DH/CD=12*6/10=7.2 дм