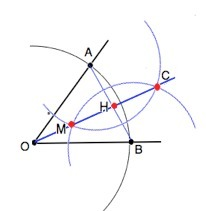
Ставим ножку циркуля в вершину О угла и проводим полуокружность, пересекающую стороны угла в т.А и В.
ОА=ОВ=R. Соединим точки А и В. Треугольник АОВ равнобедренный.
Из т. А и В как из центра раствором циркуля R больше половины расстояния АВ проводим полуокружности.
Точки их пересечения и вершина угла лежат на одной прямой. Соединяем их.
Для окружностей МС - общая хорда, АВ соединяет их радиусы. АВ и МС взаимно перпендикулярны (свойство).⇒ ОН - высота равнобедренного треугольника, следовательно, по свойству высоты равнобедренного треугольника она же – его биссектриса. Биссектриса ОС построена.