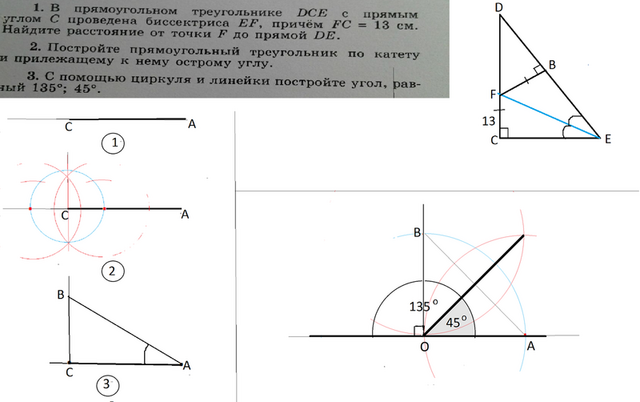
1)В прямоугольном треугольники с прямым углом С проведена биссектриса ЕF, причем FС=13 см. Найдите расстояние от точки F до прямой DЕ.
Расстояние от точки до прямой измеряется длиной проведенного к ней перпендикуляра. Пусть этот перпендикуляр FВ.
Острые углы треугольников FВЕ и FСЕ при вершине Е равны по условию, угол С=90°, угол FВЕ=90° (FВ- перпендикуляр к DЕ).FЕ- общая гипотенуза.
Если гипотенуза и острый угол одного прямоугольного треугольника равны гипотенузе и острому углу другого, такие треугольники равны.
Отсюда расстояние от F до DЕ=FС=13.см
2) Постройте прямоугольный треугольник по катету и прилежащему к нему острому углу.
Этап 1.
Начертить произвольную прямую и отложить на ней длину катета АС.
Этап 2.
Из С возвести перпендикуляр к АС. Для этого по обе стороны от С циркулем откладываем равные отрезки. Из концов этих отрезков как из центра раствором циркуля больше длины отреков начертить полуокружности так, чтобы они пересеклись по обе стороны от С. Точки пересечения соединить. Получился перпендикуляр, содержащий второй катет.
Этап 3
Из А, как из вершины, отложить с помощью транспортира известный угол. Продлить его сторону до пересечения с перпендикуляром. Точку пересечения обозначить В.
Прямоугольный треугольник АВС построен.
3) С помощью циркуля и линейки постройте угол, равный 135°; 45°
Этап 1.
Начертить произвольную прямую. Примерно на ее середине отметить точку О. Способом, указанным в предыдущей задаче, возвести из О перпендикуляр.
Этап 2.
Равным раствором циркуля на прямой и перпендикуляре отметить точки А и В. Соединить эти точки. Треугольник АОВ - прямоугольный равнобедренный по построению.Угол АОВ =90°
Этап3.
Из точек А и В раствором циркуля, равным АО=ОВ, начертить полуокружности, точки их пересечения соединить.
Соединяющий точки пересечения полуокружностей отрезок, являясь срединным перпендикуляром к АВ, пройдет через О и разделит прямой угол АОВ на два угла по 45°.
Смежный с ним больший угол равен
180°- 45°=135°
Построены два угла:45° и 135°
[email protected]