Дан треугольник АВС, у которого АВ=6 см, АС=10 см. На его сторонах взяты точки: М...

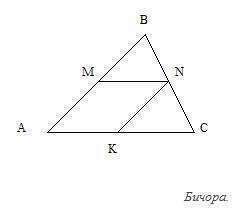
Чертеж во вложении.
1) АМNК - ромб, поэтому все его стороны равны.
2) ∆МВN ~ ∆АВС (по 2 углам- ∠В-общий, ∠BMN=∠A) =>
$\frac{MB}{AB}= \frac{MN}{AC}$
3) Пусть AM=MN=NK=AK= a (см). Тогда MB=AB-a=6-a (см).
$\frac{6-a}{6} = \frac{a}{10}$
6a=10(6-a)
60-10а=6а
16а=60
а=3,75, т.е. сторона ромба 3,75 см.
3) Pромба=4а=4*3,75=15 см
Ответ: 15 см.

Дан треугольник АВС, у которого АВ=6 см, АС=10 см. ** его сторонах взяты точки: М...