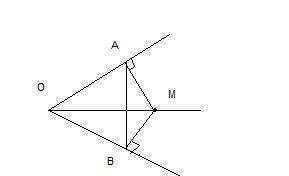
По теореме о биссектрисе угла каждая точка биссектрисы неразвернутого угла равноудалена от его сторон, значит МА=МВ.
Два прямоугольных треугольника ОАМ и ОВМ равны по гипотенузе (ОМ общая) и катетам (МА и МВ). Значит ОА=ОВ, и треугольник АОВ - равнобедренный.
По условию ОМ - биссектриса. В равнобедренном треугольнике биссектриса, проведенная к основанию, является и высотой. Значит высота ОМ перпендикулярна основанию АВ.