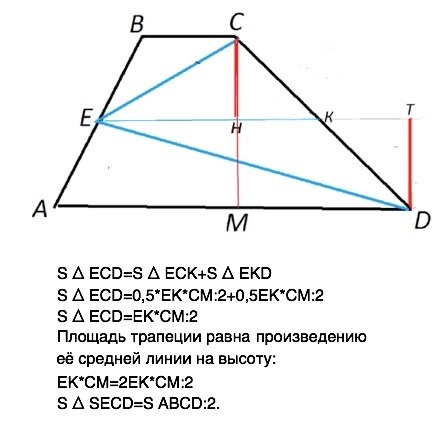
Сделаем рисунок.
От середины АВ проведем ЕК - среднюю линию трапеции.
ЕК делит треугольник ЕСD на два:ᐃ ЕСК и ᐃ ЕКD.
ЕК по свойству средней линии делит высоту СМ трапеции пополам,
и СН=МН=DТ=0,5*СМ (см. рисунок)
Треугольники ЕСК и ЕКD равновелики: площадь каждого равна
половине произведения их общего основания ЕК, являющегося
средней линией трапеции АВСD, на половину её высоты.
S ᐃ ECD=S ᐃ ECK+S ᐃ EKD
S ᐃ ECD=0,5*EK*CM:2+0,5EK*CM:2
S ᐃ ECD=EK*CM:2
Площадь трапеции равна произведению её средней линии на высоту.
ЕК*СМ=2EK*CM:2
S ᐃ SECD=S ABCD:2, что и требовалось доказать.