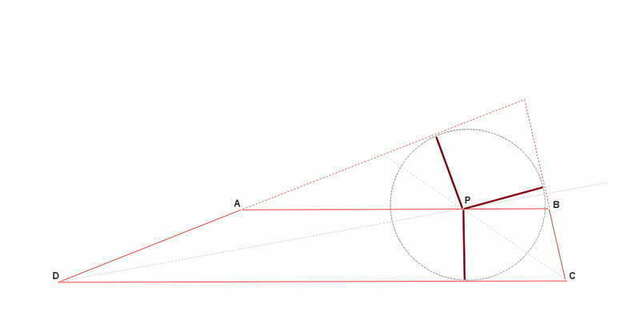
Если достроить трапецию до треугольника,
то точка Р -- центр вписанной в этот треугольник окружности
(((центр вписанной в треугольник окружности = точка пересечения биссектрис)))
расстояния до этих прямых --- это радиусы...
единственное, Вы не указали АВ -- это основание или боковая сторона...
если АВ -- боковая сторона трапеции, то окружность окажется заключенной между параллельными основаниями трапеции...
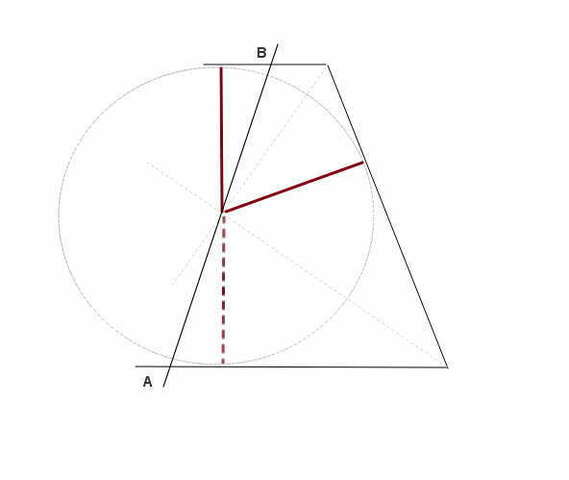
и эта окружность будет вписана в углы C и D ((т.к. центр окружности --- пересечение биссектрис этих углов)))
биссектриса = это геометрическое место точек, равноудаленных от сторон угла...
т.е. точка, лежащая на биссектрисе угла ADC равноудалена от AD и DC
точка, лежащая на биссектрисе угла DCВ равноудалена от DС и CВ...