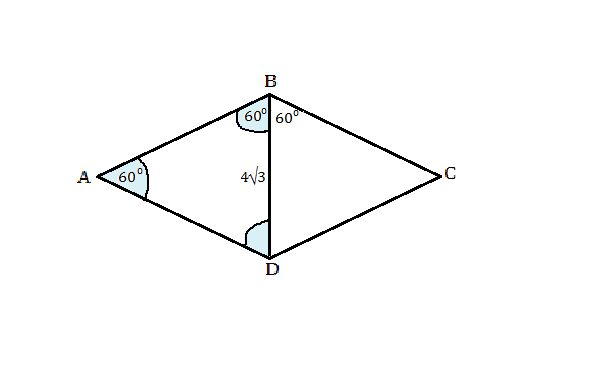
В ромбе, как в любом параллелограмме, сумма углов при одной стороне равна 180º, и имеются 2 пары углов : 2 острых и 2 тупых.
Меньшая диагональ противолежит меньшему углу. Пусть это будет угол А.
Пусть меньшая диагональ будет BD. Тогда треугоьник АВD- равносторонний. т.к. все его углы равны 60º. ⇒ все стороны равны 4√3
Площадь параллелограмма ( и ромба в том числе) равна произведению его сторон, умноженному на синус угла между ними.
S=a²*sin(60º)=(4√3)²*√3):2=24√3 (единиц площади)