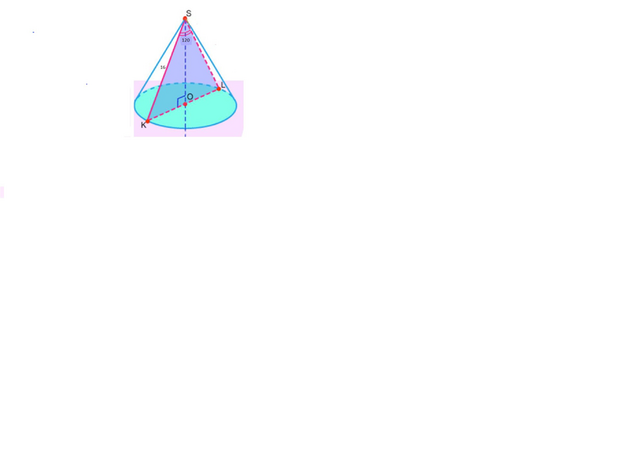
- высота конуса

- образующие конуса

- радиусы
Δ

- осевое сечение конуса

- угол при вершине осевого сечения конуса



см

Рассмотрим осевое сечение конуса:
Δ

- равнобедренный треугольник, так как

см

высота, медиана и биссектриса Δ

,
т. е.

⊥


и

Δ

прямоугольный (

)

, значит
 Катет прямоугольного треугольника, лежащий против угла в 30 градусов, равен половине гипотенузы.
Катет прямоугольного треугольника, лежащий против угла в 30 градусов, равен половине гипотенузы.
Значит


см
По теореме Пифагора найдем


см

см³
Ответ:

см³