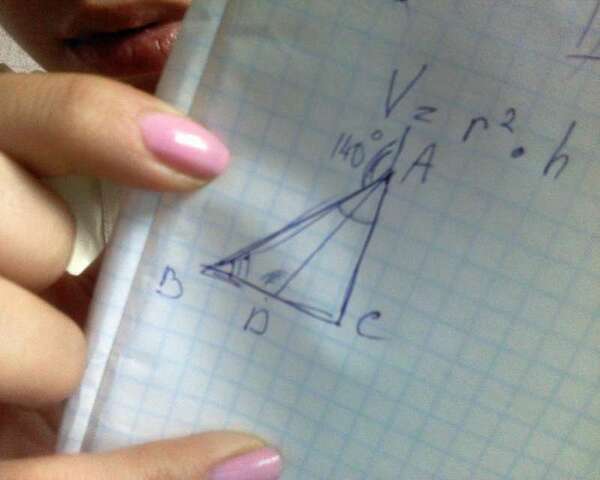
Смотри на фото.
Нам нужно найти углы ΔBAD. Нам известен внешний угол от угла А, равный 140°. Если 180°-140° получим угол А, который равен 40°. А т.к. АD - биссектриса ⇒ угол BAD = половине угла А, т.е. = 20°.
Найдем угол В. Для этого вычтем из 180° углы А и С. 180°-90°-40°=30° - угол В.
И найдем угол ВDА. 180°- 20°-30°=130°
Ответ: угол В = 30°, угол BAD = 20°, и угол BDA = 130°