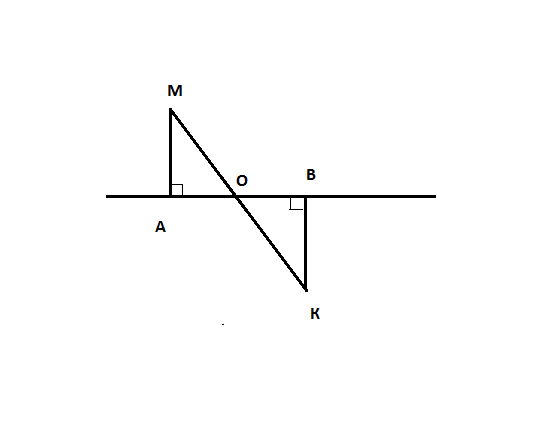По условию АМ и ВК - перпендикуляры. Две прямые, перпендикулярные к третьей, не пересекаются, значит
AMIIBK.
АМ=ВК по условию
Значит, треугольники АОМ и ВОК равны по второму признаку равенства: сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника.