7. Точка M одинаково удалена от всех сторон квадрата ABCD. Расстояние от точки M до...

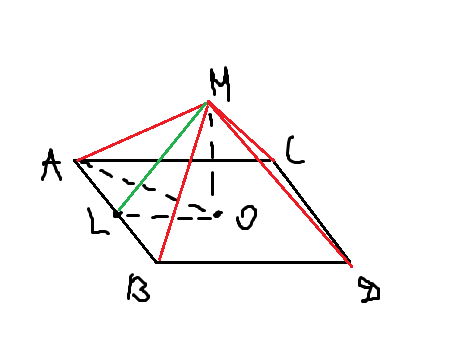
Дано: ABCD - квадрат, ОМ=16см, AB=24см

Решение: точка $M$ лежит на перпендикуляре к плоскости квадрата, проходящем через его центр - точку $O$ .

Так как $O$ - центр симметрии квадрата, то расстояние от точки $O$ до сторон будет равно половине длины стороны, а до вершин - половине диагонали.

Отметим точку $L$ - середину стороны $AB$ . Рассмотрим $\Delta LOM$ . Он будет прямоугольным, сторона $ОМ$ известна, $OL=\frac{AB}{2}=12$ . По теореме о трех перпендикулярах, $LM \perp AB$ , а значит $LM$ - расстояние от точки $M$ до стороны $AB$ . По теореме Пифагора, $LM=\sqrt{OL^2+OM^2}=\sqrt{144+256}=20$

Теперь найдем диагональ $AD$ :
$AD=\sqrt{24^2+24^2}=24\sqrt{2}$ . Соответственно, половина диагонали $AO=12\sqrt{2}$ . Воспользуемся теоремой Пифагора для треугольника $\Delta AOM$ :
$AM=\sqrt{AO^2+OM^2}=\sqrt{(12\sqrt{2})^2+16^2}=\sqrt{288+256}=\\ =\sqrt{544}=4\sqrt{34}$

Ответ: $20; 4\sqrt{34}$