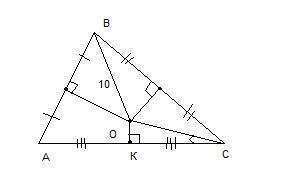
Рассмотрим треугольник ВОС. Он равнобедренный, т.к. точка О как каждая точка серединного перпендикуляра к отрезку ВС равноудалена от концов этого отрезка. Значит
ВО=ОС=10 см
В прямоугольном треугольнике СКО катет ОК (его длину нам нужно найти как расстояние от точки О до стороны АС) лежит против угла в 30 градусов. Значит, он равен половине гипотенузы ОС:
ОК=ОС : 2 = 10 : 2 = 5 см