Найти число решений уравнения 2cos^2 x-5sinx=4 ** отрезке [0;5П/2]помогите пожалуйста, и...

Question

Найти число решений уравнения 2cos^2 x-5sinx=4 на отрезке [0;5П/2]
помогите пожалуйста, и если можно, разъясните поподробнее решение таких уравнений

Answer 1

 2cos^2x - 5sinx = 4 
 2*( 1 - sin^2x) - 5sinx - 4  = 0 
2 - 2sin^2x - 5sinx - 4 = 0 
-  2sin^2x - 5sinx - 2 = 0    /:(-1)
2sin^2x + 5sinx + 2 = 0 

Пусть sinx = t, t ∈ [ - 1; 1] 
Имеем: 
2t^2 + 5t + 2 = 0 
Решим кв. уравнение
D= 25 - 4*4 = 25 - 16 = 9 =  3^2
t₁ = ( - 5 +3)/4 = - 1/2
t₂ = ( - 5 - 3)/4 = - 2 ==> не удовлетворяет условию 

Произведём обратную замену, получим
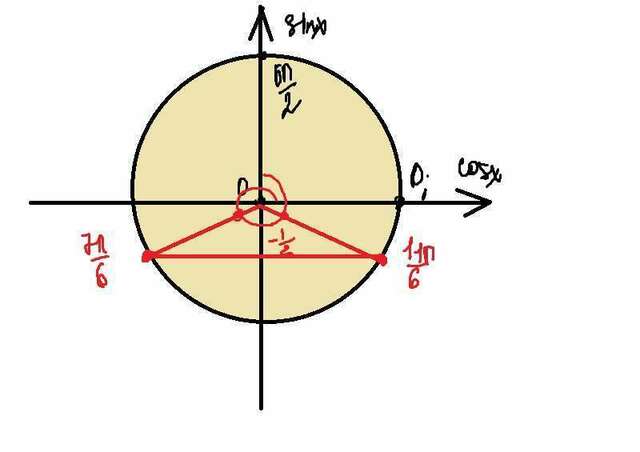
sinx = - 1/2
x = - pi/6 + 2pik
x = 7pi/6 + 2pik

+ ОТБОР НА ОКРУЖНОСТИ
========================

---