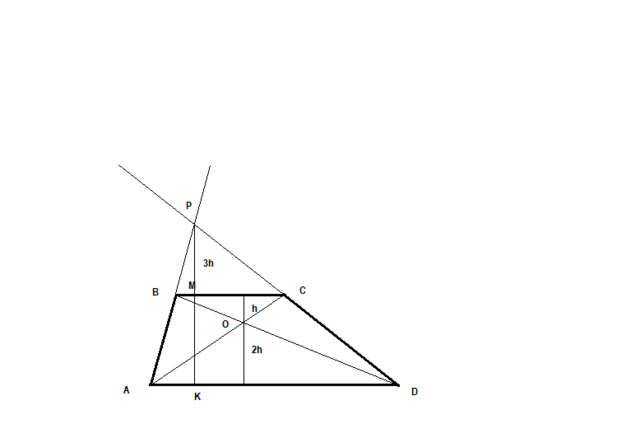
пусть h- высота треугольника BOC
тогда 2h - высота треугольника AOD - из подобия BOC и AOD
тогда высота трапеции МК=h+2h =3h
из подобия BPC и APD следует
PK/PM = AD /BC= 2
тогда PK=6h => РМ=3h
площадь треугольника BOC 1/2*ВС*h= 3 (1)
площадь треугольника BPC 1/2*ВС*3h=3*(1/2*ВС*h)= S (2)
подставим (1) в (2) S=9
тогда
площадь четырёхугольника BOCP = пл тр BOC + пл тр BPC = 3+9=12