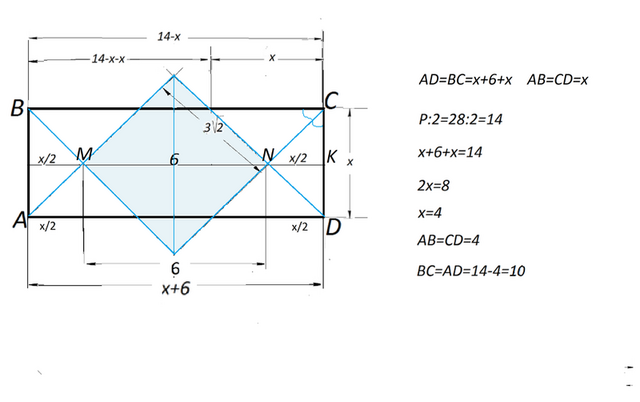
Решение (см рисунок)
Биссектриса любого угла параллелограмма отсекает от него равнобедренный треугольник.
Прямоугольник - параллелограмм.
4 биссектрисы отсекают от него равнобедренные прямоугольные треугольники с катетами, равными меньшей стороне.
Прямоугольник, образованный пересечением биссектрис - квадрат (равенство его сторон нетрудно доказать).
Периметр этого квадрата равен 12√3, каждая его сторона 3√2,
диагональ - 3√2*√2=6
Полупериметр прямоугольника равен 28:2=14.
Пусть АВ=СД=х,
тогда ВС=АД= 14-х
Соединим середины АВ и СД отрезком, параллельным АD.
Средняя его часть-диагональ получившегося пересечением биссектрис квадрата, а боковые части - медианы половин отсечённых биссектрисами треугольников
и равны х:2 - половине меньшей стороны прямоугольника .
Большая сторона равна х/2+х/2+6=х+6
Р:2=(х+х+6)=14
2х=8
х=4
АВ=CD=4 меньшая сторона прямоугольника
BC=AD=14-4=10
--------
[email protected]