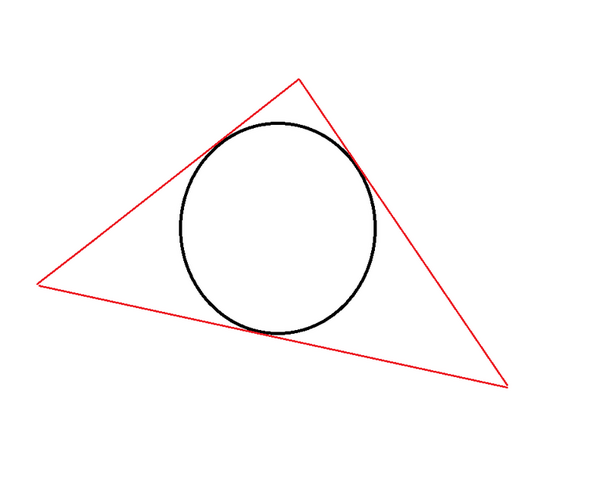
Сделаем рисунок по условию
окружность вписана в треугольник
Все стороны треугольника касаются окружности
на основании Свойства касательной:
Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
пусть DB=BE = x
тогда
ЕС = FC = a - x
AD = AF = c - x
AC = AF +FC = a - x + c - x = a+c -2x (1)
Но также
АС =b (2)
тогда
b = a+c -2x
2x = a+c -b
x = (a+c-b) /2
BD=BE= = ( a+c-b) /2
AD=AF= c - x = c - (a+c-b) /2 = ( - a+b+c) /2
EC=FC= a - x = a - (a+c-b) /2 = ( a+b-c) /2