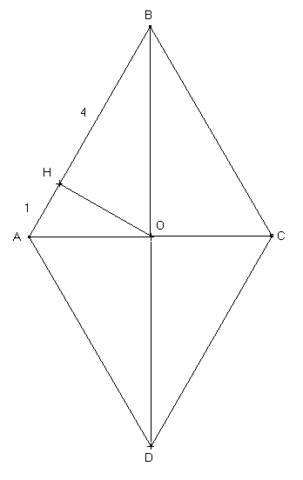
Диагонали ромба делят его на четыре равных прямоугольных треугольника, поэтому достаточно найти площадь одного из них (см. рисунок). В треугольнике AOB высота OH делит гипотенузу AB на отрезки, равные 1 и 4. Известно, что высота прямоугольного треугольника, опущенная на гипотенузу, равна среднему геометрическому длин отрезков, на которые она делит гипотенузу. (Этот факт, насколько мне известно, не нужно доказывать, но это легко сделать, так как треугольники AOH и BOH подобны, поэтому AH/OH=OH/BH). Тогда OH=√AH*BH=2. Зная длину гипотенузы и длину высоты, опущенной на неё, можно найти площадь треугольника, которая равна 1/2*(4+1)*2=5. А площадь ромба, то есть площадь 4 таких треугольников, равна 5*4=20.