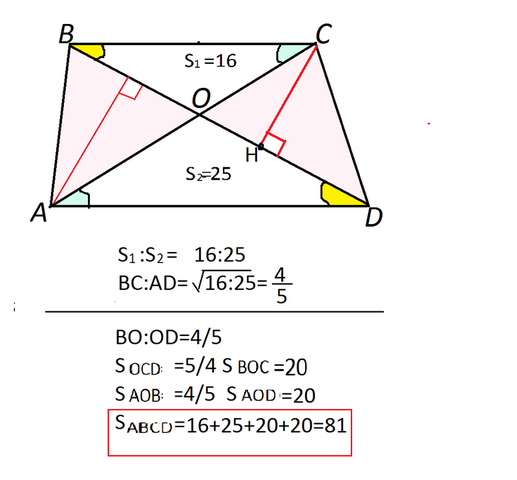
Вспомним, что в трапеции треугольники, образованные основаниями и пересекающимися диагоналями подобны по трём равным углам.
S ВОС: S AOD=16:25
Отношение площадей подобных фигур равно квадрату коэффициента их подобия. Следовательно,
k=ВО:ОD=√(16:25)=4/5
Отношение площадей треугольников с равными высотами равно отношению их оснований.
Треугольнике ВОС и СОD имеют общую высоту. Следовательно, площадь треугольника СО=5/4 площади ВОС и равна 16:4*5=20
В трапеции треугольники, образованные боковыми сторонами и пересекающимися диагоналями равновелики. ⇒
S AOB=S COD=20 ( можно проверить по отношению ВО:ОD и равным высотам).
Площадь трапеции равна
S ABCD= S BOC+S AOD+S AOB+S COD=16+25+20+20=81