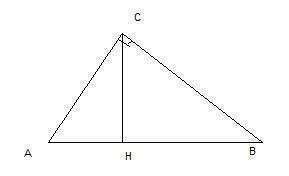
1. Пусть угол АСН равен х, тогда угол НСВ, вдвое его больший, равен 2х. Зная, что сумма этих углов равна 90°, запишем:
х + 2х = 90
3х = 90
х = 30
Значит, < АСН = 30°, < НСВ = 30*2 = 60°
2. В прямоугольном треугольнике СНВ находим угол В:<В = 180 - <HCB - < CHB = 180 - 60 - 90 = 30°<br>3. Зная, что катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы, можно записать:
АН = 1/2АС (в треугольнике АНС),
АС = 1/2АВ (в треугольнике АВС), отсюда АВ = 2АС.
4. Выразим НВ:
НВ = АВ - АН = 2АС - 1/2АС = 3/2АС
5. Запишем отношение НВ к АН:
НВ/АН = 3/2АС : 1/2АС = 3/1