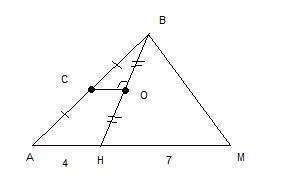
1. Зная, что отрезок АМ разбит на 4+7=11 частей, находим длину одной части: 22:11=2 см, значит
АН=4*2=8 см
2. Рассмотрим треугольник АВН: СО здесь - средняя линия, поскольку соединяет середины сторон. Значит, СОIIАН и СО=1/2АН,
СО=8/2=4 см
3. Треугольники СВО и АВН подобны по второму признаку подобия: две стороны одного треугольника пропорциональны двум сторонам другого и углы, заключенные между этими сторонами, равны. В нашем случае:
ВС/ВА=ВО/ВН=1/2, а угол В - общий. Значит, углы подобных треугольников соответственно равны, и
<ВОС=<ВНА=105°<br>4. Зная, что развернутый угол АНМ равен 180°, находим угол ВНМ:
<ВНМ=</strong>180-<ВНА=180-105=<strong>75°