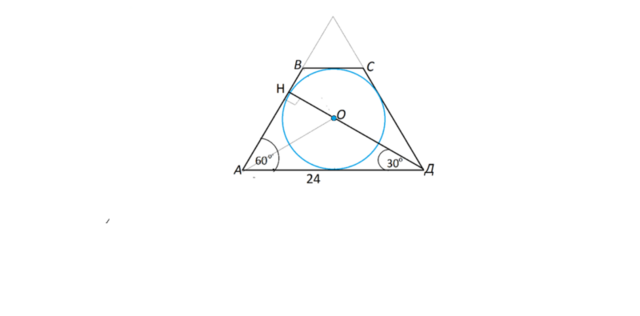
Дана равнобедренная трапеция с острым углом 60 градусов и большим основным равным 24. Прямая проходящая через вершину острого угла и центр вписанной окружности делит трапецию на четырехугольник и треугольник.
Найдите площадь полученного треугольника
.
Обозначим вершины трапеции
АВСД.
Углы равнобедренной трапеции, прилежащие к основанию, равны.
Следовательно, угол
ВАД=СДА=60°
Продолжим боковые стороны до их пересечения и получим
равносторонний треугольник.
.Центр вписанной в треугольник окружности лежит на пересечении его высот (биссектрис)
Прямая
, проходящая через вершину острого угла и центр вписанной окружности
, делит угол при основании трапеции пополам
, т.к. является биссектрисой угла
.
Следовательно
, треугольник АНД - половина правильного треугольника, и его площадь равна половине площади правильного треугольника со стороной 24.
Площадь правильного треугольника находят по формуле
S=(a²√3):4
S ⊿ АДН=
¹/₂(24²√3):4= 576(√3)
:8=
72√3
-----------------
Есть и другие способы решения, ответ будет тот же, но это решение - самое, на мой взгляд, короткое.