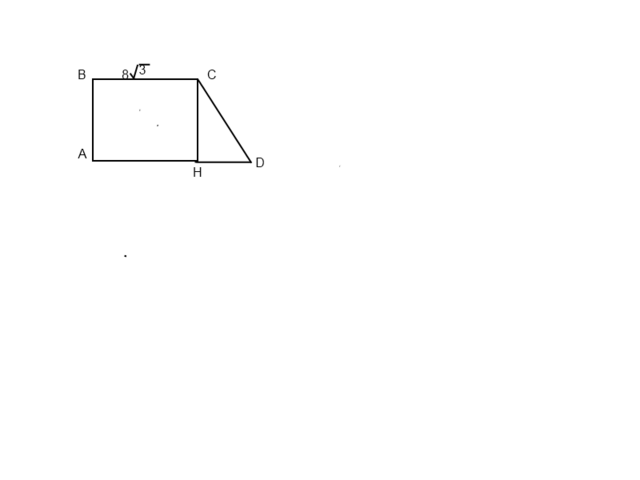
треугольник CDH прямоугольный. угол CDH=30 градусов => что CH=1/2 CD.
пусть CH=x ,тогда CD=2х. AB -высота. СН=АВ. АВ+CD=36 получаем что CD+CH=36. значит x+2x=36. отсюда х=12. высота найдена. найдем боковую сторону: 36-CH. СD=36-12=24. тк треугольник CDH прямоуг. тогда DH найдем по теореме пифагора: DH^{2}=CD^{2}-CH^{2}. получаем DH^{2}=24^{2}-12^{2}=576-144=432. DH=12\sqrt{3}. найдем нижнее(оно же большее основание) 8\sqrt{3}+12\sqrt{3}=20\sqrt{3}. найдем площадь трапеции: S=1/2*AD*BC. S= 1/2*8\sqrt{3}*20\sqrt{3}=240.
Ответ: площадь S=240, высота AB=12.