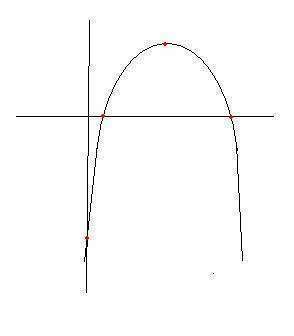
y = -x² + 4x - 1 - это парабола, ветви которой направлены вниз
для нахождения вершины производную приравниваем к нулю
у' = -2x + 4 = 0
2x = 4
x = 2
y(2) = -4 + 8 - 1 = 3
Вершина параболы смещена в точку (2; 3)
Для нахождения точек пересечения с осью ОХ решим уравнение
-х² +4x -1 = 0
x² - 4x +1 = 0
D = 16 - 4 = 12
x1 = 2 + √3 ≈ 3,7
x2 = 2 - √3 ≈ 0,3
Точки пересечения (2-√3; 0) и (2+√3; 0)
Точка пересечения с осью ОУ (0; -1)