Нужно найти наименьшее значение функции y=x^3-4x^2-3x+2 на отрезке [2;5], и распишите...

1. Для начала, нужно найти производную функции:

$f ' (x^{3}-4x^2-3x+2) = 3x^2-8x-3$

2. Затем нужно прировнять производную к нулю:

$3x^2-8x-3 = 0 \\ D = b^2 - 4ac = 64 + 4*3*3 =100$

$x1 = \frac{8+ 10}{6}= 3 \\ x2 = \frac{8-10}{6} = -\frac{1}{3}$

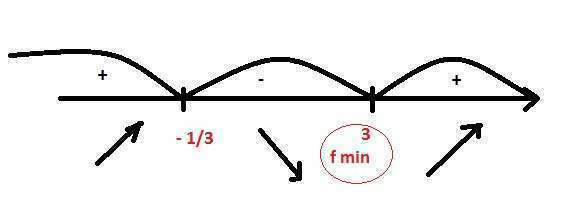
3. Далее по методу интервалов найти "критические" точки функции (экстремумы)

см. картинку.

4. И наконец, находишь наименьшее значение функции (нужно вместо x подставить 3 )

$y = x^3-4x^2-3x+2, x = 3 \\ y = 3^3 - 4*3^3 - 3*3 = - 18$

$f min = -18, x = 3$

Нужно найти наименьшее значение функции y=x^3-4x^2-3x+2 ** отрезке [2;5], и распишите...