Если дать только чертежи - ответ будет считаться нарушением. Можно ведь и не читать решение, а использовать только чертежи, данные во вложении. .
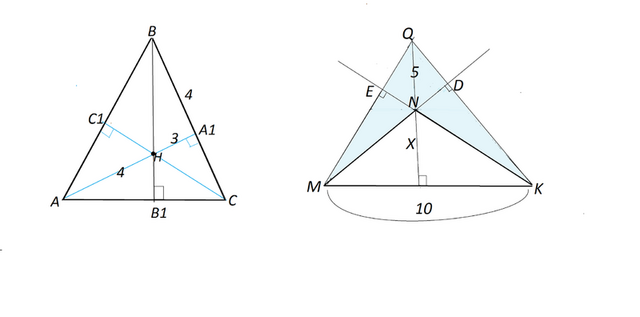
Задача 1.
Необходимо найти ВВ1.
ВВ1=ВН+НВ1
ВН можно найти по т. Пифагора, а можно вспомнить, что гипотенуза треугольника с катетами 3 и 4 - равна 5 (
египетский треугольник).
В прямоугольных треугольниках АНВ1 и ВНА1 имеется по равному острому углу ( вертикальные при Н)
⇒ они подобны.
ВН
:АН=НА1
:НВ1
5:4=3:НВ1
НВ1=12
:5=2
,4
ВВ1=5+2,4=
7,4
Задача 2
Так как треугольник тупоугольный, пересечение высот треугольника будет находиться вне его.
И тогда площадь четырехугольника MNKQ, окрашенного на рисунке в голубой цвет, равна разности площадей треугольника MQK и треугольника MNK
Высоты треугольника (или их продолжения) пересекаются в одной точке. Здесь эта точка - Q.
Пусть высота треугольника MNK будет
х,
тогда высота треугольника MQK -
х+5
S MQK=10(x+5)
:2
S MNK=10x
:2
S MNKQ=10(x+5)
:2-10x
:2=
5(х+5)-5х
S MNKQ =5х+25-5х=
25
--------------
[email protected]