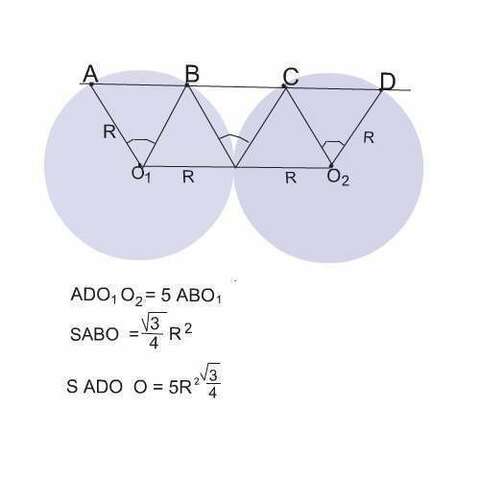
Соединим центры окружостей последовательно с А, В, С и D (cм. рисунок).
Получим 5 треугольников.
Поскольку АВ=ВС=СD, отрезки АВ и СD отсекают от окружностей равные дуги.
Потому центральные углы при них равны. Расстояния от центров окружности до прямой АD равны, как расстояние от центра до равных хорд.
=> АD и О₁О₂ параллельны. По свойству параллельных прямых все углы в полученных 5 треугольниках равны. Треугольники равносторонние.
Площадь равностороннего треугольника, выраженного через его сторону, равна
S=(а²√3):4.
Треугольников таких в данном четырехугольника 5, а сторона их равна радиусу.
Искомая площадь равна
S=(5R²√3):4