На каком расстоянии от фонаря ( в метрах) стоит человек ростом 1,8 м, если длина его тени...

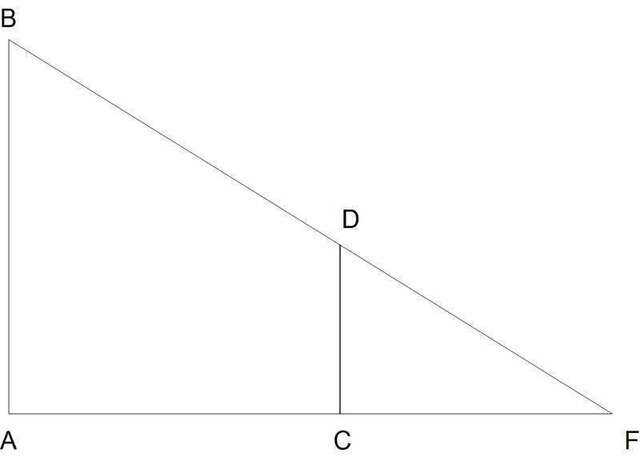
Пусть CD - человек, AB - фонарь, CF - тень человека

Тогда: CD=1,8; AB=5; CF=9

Требуется найти: AС

1) Рассмотрим треугольники ABF и CDF - они подобны (общий угол F и равные углы FCD и FAB (прямые))

2) Из подобия следует отношение сторон:

$\frac{AB}{CD}=\frac{AF}{CF}$

Подставим известные значения:

$\frac{5}{1,8}=\frac{AF}{9}$

Найдём AF: $AF=\frac{5 \cdot 9}{1,8}=25$

AC=AF-CF=25-9=16

** каком расстоянии от фонаря ( в метрах) стоит человек ростом 1,8 м, если длина его тени...