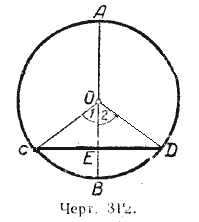
Пусть диаметр АВ перпендикулярен к хорде СD (черт. 312). Требуется доказать, что СЕ = ЕD, СВ = ВD, СА = DА.
Соединим точки С и D с центром окружности О. В равнобедренном треугольнике СОD отрезок ЕО является высотой, проведённой из вершины О на основание СD; следовательно, ОЕ является и медианой и биссектрисой, т. е. СЕ = ЕD и / 1 = / 2. Но / 1 и / 2 суть центральные углы. Отсюда равны и соответствующие им дуги, а именно СВ = ВD. Дуги СА и ВА также равны между собой, как дополняющие равные дуги до полуокружности.