Трапеция ABCD с основаниями AD и BC вписана в окружность с диаметром AD. Найти углы...

Question

Трапеция ABCD с основаниями AD и BC вписана в окружность с диаметром AD. Найти углы трапеции, если ее диагонали пересекаются под углом 40 градусов.

Answer 1

в окружность можно вписать только равнобедренную трапецию 

пусть диагонали пересекаются в точке О. угол АОВ=СОД=40 градусов (условие)

значит, угол ВОС=АОД= 180-40=140 градусов (смежны с аов и сод)

т.к АД - диаметр, то угол АСД=АВД=90 градусов

угол ОДС, угол ВАО = 90-40=50 градусов

для треугольника АОД угол АОВ - внешний, зачит равен сумме углов не смежных с ним. т.е. угол ОАД=ОДА (св-во равнобедр. трапеции) = 40/2=20 градусов

и затем, чтобы найти угол ОВС и ВСО воспользуемся тем же внешним углом, те углы по 20 градусов.

в итоге, угол Д= 20+50=70 градусов

             угол С= 90+20=110 градусов 

слишком длинное решение, можно и проще, наверное, но главное - правильно нарисовать. удачи! 

Answer 2

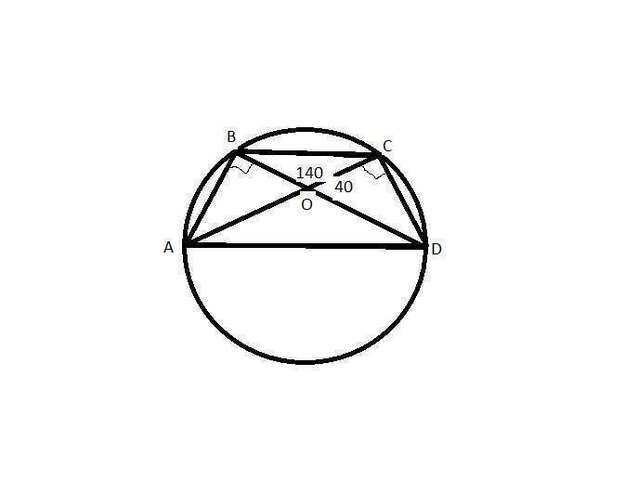
Дано: трапеция АВСD, AD - диаметр, AD, BC - основания, точка О - точка пересечения диагоналей, угол СОD = угол АОВ = 40 градусов

Найти: углы трапеции

 

Решение: так как трапеция вписана в окружность, то, следовательно, трапеция равнобедренная, поскольку только равнобедренную трапецию можно вписать в окружность, значит АВ=СD. 

Углы АВD и DCA опираются на диаметр, значит эти углы прямые.

Углы СОВ и АОD как вертикальные углы равны, к тому же они равны (360-(40*2))/2=140 градусов. 

Трапеция равнобедренная, значит точка пересечения диагоналей делит их на попарно равные отрезки, согласно свойству равнобедренной трапеции. Следовательно, треугольники ВОС и АОD равнобедренные по определению. А значит, углы ОВС, ОСВ, ОАD и DОА равны по (180-140)/2=20 градусов. 

Треугольники ВОА и ОСD прямоугольные из решения, причём в них один угол равен 40 градусов, значит углы ОАВ и ОDC равны по 50 градусов.  

Ну и считаем: угол АВС=угол ВСD=90+20=110 градусов, угол ВАD = угол АDC = 20+50=70 граудсов. 

Ответ: 70 и 110.  

---